문제
N(2≤N≤10,000)개의 섬으로 이루어진 나라가 있다. 이들 중 몇 개의 섬 사이에는 다리가 설치되어 있어서 차들이 다닐 수 있다.
영식 중공업에서는 두 개의 섬에 공장을 세워 두고 물품을 생산하는 일을 하고 있다. 물품을 생산하다 보면 공장에서 다른 공장으로 생산 중이던 물품을 수송해야 할 일이 생기곤 한다. 그런데 각각의 다리마다 중량제한이 있기 때문에 무턱대고 물품을 옮길 순 없다. 만약 중량제한을 초과하는 양의 물품이 다리를 지나게 되면 다리가 무너지게 된다.
한 번의 이동에서 옮길 수 있는 물품들의 중량의 최댓값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N, M(1≤M≤100,000)이 주어진다. 다음 M개의 줄에는 다리에 대한 정보를 나타내는 세 정수 A, B(1≤A, B≤N), C(1≤C≤1,000,000,000)가 주어진다. 이는 A번 섬과 B번 섬 사이에 중량제한이 C인 다리가 존재한다는 의미이다. 서로 같은 두 도시 사이에 여러 개의 다리가 있을 수도 있으며, 모든 다리는 양방향이다. 마지막 줄에는 공장이 위치해 있는 섬의 번호를 나타내는 서로 다른 두 정수가 주어진다. 공장이 있는 두 섬을 연결하는 경로는 항상 존재하는 데이터만 입력으로 주어진다.
출력
첫째 줄에 답을 출력한다.
푸는데 적어도 하루는 걸린 문제, 이분 탐색과 bfs 를 짬뽕한 문제였다. 이분탐색하면서 bfs 가 참이면 갱신하는 문제
풀어서 기쁘다.
문제 난이도 : 중상
문제유형: 이진탐색
추천 풀이 시간: 1-2 시간
문제 풀이 핵심 아이디어
다리 개수 M은 최대 100,000이고, 중량제한 C 는 최대 1,000,000,000(10억 -> 로그나 루트를 씌워야함.)이다.
이진 탐색을 이용해서 O(M* logC) 네 문제를 해결할 수 있습니다.
한 번의 이동에서 옮길 수 있는 물품들의 중량의 최댓값을 이진탐색으로 찾는다.
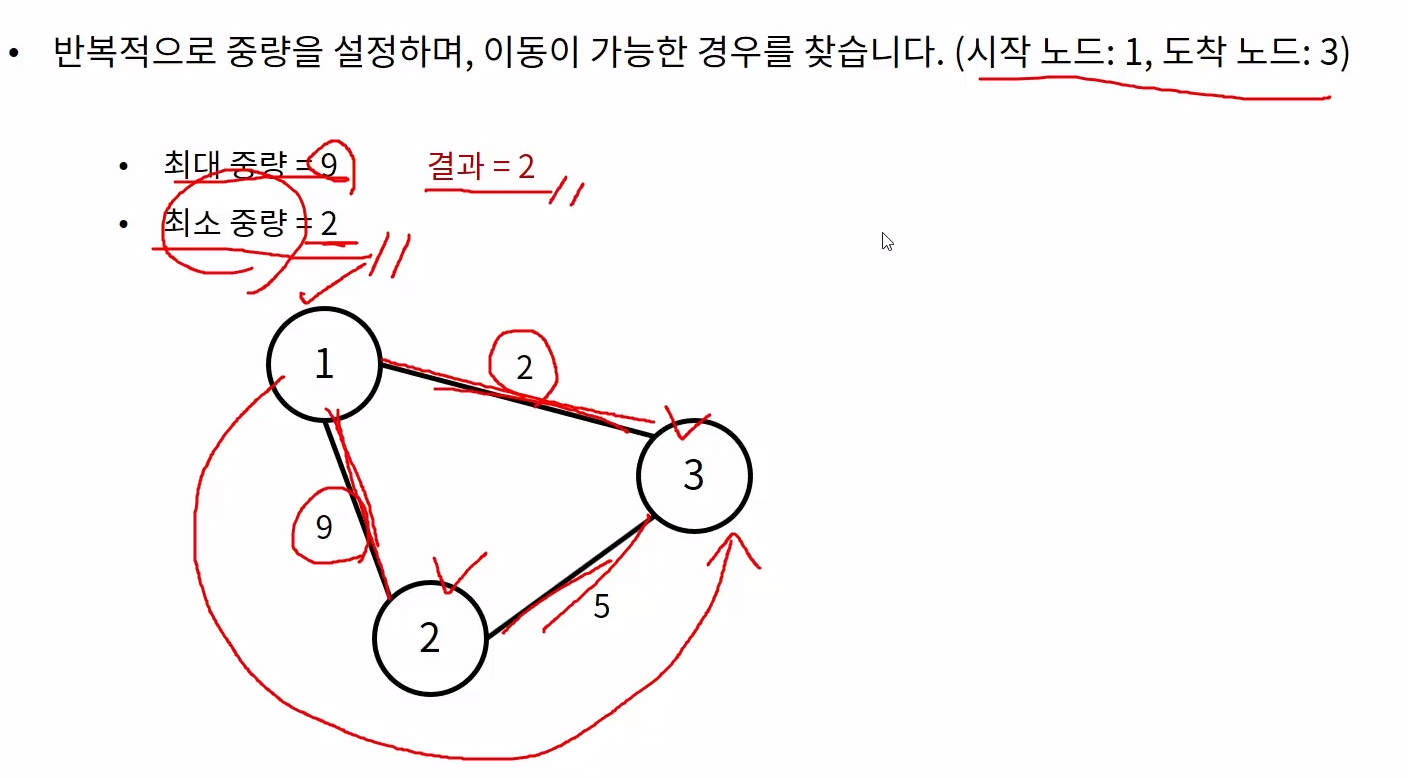
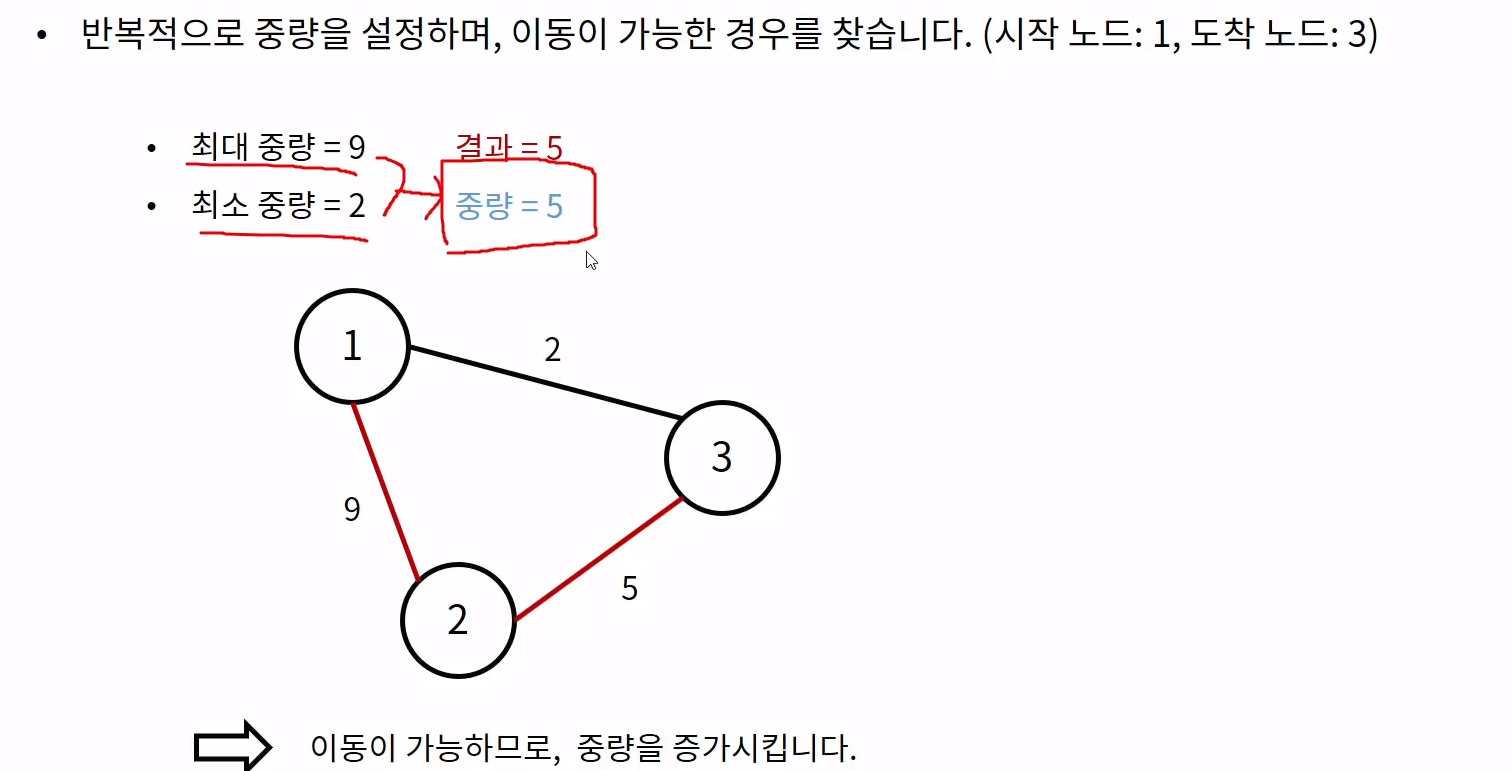


# 내 풀이
import collections
import math
def bfs(start,endm):
visit=[start]
will_visit=collections.deque(graph[start])
while will_visit:
travel = will_visit.popleft()
if travel == end:
return True
if travel not in visit:
visit.append(travel)
for i in graph[travel]:
will_visit.append(i)
#will_visit.extend(graph[travel])
return False
N, M = map(int, input().split())
#graph={}
graph_cost=[]
#for i in range(1, N+1):
# graph[i]=set()
for _ in range(M):
lis=list(map(int, input().split()))
#graph[lis[0]].append(lis[1])
#graph[lis[1]].append(lis[0])
graph_cost.append([lis[2], [lis[1], lis[0]]])
graph_cost.sort()
start, end = map(int, input().split())
maxi= graph_cost[-1][0]
mini = graph_cost[0][0]
mid_list=[]
answer=0
#print(graph_cost)
while maxi>=mini:
# print(answer)
mid = math.ceil((maxi+mini)/2)
#print(maxi, mini, mid)
if mid not in mid_list:
mid_list.append(mid)
filtered = list(filter(lambda a:a[0]>=mid, graph_cost))
graph={}
for i in range(1, N+1):
graph[i]=[]
for f in filtered:
graph[f[1][0]].append(int(f[1][1]))
graph[f[1][1]].append(int(f[1][0]))
#print('graph', graph)
if bfs(start, end):
answer=max(answer, mid)
mini = mid-1
else:
maxi=mid+1
else:
mini+=1
print(answer)
# 동빈나
from collections import deque
n,m = map(int, input().split())
adj =[[] for _ in range(n+1)]
def bfs(c):
queue = deque([start_node])
visit = [False] *(n+1)
visit[start_node]=True
while queue:
x= queue.popleft()
for y, weight in adj[x]:
if not visited[y] and weight >=c:
visited[y]=True
queue.append(y)
return visited[end_node]
start = 100000000000000
end =1
for _ in range(m):
w,y,weight = map(int, input().split())
adj[x].append((y, weight))
adj[y].append((x,weight))
start = min(start, weight)
end = max(end, weight)
start_node , end_node = map(int, input().split())
result = start
while(start<=end):
mid = (start+ end) //2 # mid 는 현재의 중량을 의미
if bfs(mid): # 이동이 가능하므로 중량을 증가시킵니다.
result = mid
start =mid+1
else: # 이동이 불가능하므로 중량을 감소시킵니다.
end = mid -1
print(result)
'알고리즘' 카테고리의 다른 글
| 백준 1003번 피보나치 함수 파이썬+ 메모제이션 (0) | 2020.10.04 |
|---|---|
| 백준 2748번 피보나치수 2 : 다이나믹 프로그래밍 (0) | 2020.10.04 |
| 코딜리티 PermMissingElem (0) | 2020.10.03 |
| 코딜리티 스텝 2 : dict filter (0) | 2020.10.03 |
| 코딜리티 BinaryGap 파이썬 :level 1 (0) | 2020.10.03 |
