문제
이진트리를 다음의 규칙에 따라 행과 열에 번호가 붙어있는 격자 모양의 틀 속에 그리려고 한다. 이때 다음의 규칙에 따라 그리려고 한다.
- 이진트리에서 같은 레벨(level)에 있는 노드는 같은 행에 위치한다.
- 한 열에는 한 노드만 존재한다.
- 임의의 노드의 왼쪽 부트리(left subtree)에 있는 노드들은 해당 노드보다 왼쪽의 열에 위치하고, 오른쪽 부트리(right subtree)에 있는 노드들은 해당 노드보다 오른쪽의 열에 위치한다.
- 노드가 배치된 가장 왼쪽 열과 오른쪽 열 사이엔 아무 노드도 없이 비어있는 열은 없다.
이와 같은 규칙에 따라 이진트리를 그릴 때 각 레벨의 너비는 그 레벨에 할당된 노드 중 가장 오른쪽에 위치한 노드의 열 번호에서 가장 왼쪽에 위치한 노드의 열 번호를 뺀 값 더하기 1로 정의한다. 트리의 레벨은 가장 위쪽에 있는 루트 노드가 1이고 아래로 1씩 증가한다.
아래 그림은 어떤 이진트리를 위의 규칙에 따라 그려 본 것이다. 첫 번째 레벨의 너비는 1, 두 번째 레벨의 너비는 13, 3번째, 4번째 레벨의 너비는 각각 18이고, 5번째 레벨의 너비는 13이며, 그리고 6번째 레벨의 너비는 12이다.
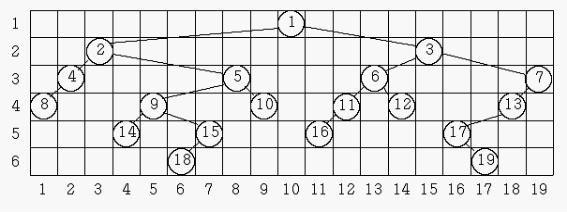
우리는 주어진 이진트리를 위의 규칙에 따라 그릴 때에 너비가 가장 넓은 레벨과 그 레벨의 너비를 계산하려고 한다. 위의 그림의 예에서 너비가 가장 넓은 레벨은 3번째와 4번째로 그 너비는 18이다. 너비가 가장 넓은 레벨이 두 개 이상 있을 때는 번호가 작은 레벨을 답으로 한다. 그러므로 이 예에 대한 답은 레벨은 3이고, 너비는 18이다.
임의의 이진트리가 입력으로 주어질 때 너비가 가장 넓은 레벨과 그 레벨의 너비를 출력하는 프로그램을 작성하시오
입력
첫째 줄에 노드의 개수를 나타내는 정수 N(1 ≤ N ≤ 10,000)이 주어진다. 다음 N개의 줄에는 각 줄마다 노드 번호와 해당 노드의 왼쪽 자식 노드와 오른쪽 자식 노드의 번호가 순서대로 주어진다. 노드들의 번호는 1부터 N까지이며, 자식이 없는 경우에는 자식 노드의 번호에 -1이 주어진다.
출력
첫째 줄에 너비가 가장 넓은 레벨과 그 레벨의 너비를 순서대로 출력한다. 너비가 가장 넓은 레벨이 두 개 이상 있을 때에는 번호가 작은 레벨을 출력한다.
문제 난이도 : 중
문제 유형: 트리 구현
추천 풀이 시간 : 50분
중위 순회를 이용하면, x 축을 기준으로 왼쪽으로부터 방문한다는 특징이 있습니다.
이 문제는 중위 순회 알고리즘을 이용하고, 추가적으로 level 값을 저장하도록 하여 문제를 해결할 수 있습니다.
class Node:
def __init__(self,number, left, right):
self.parent = -1
self.number = number
self.left = left
self.right = right
def in_order(node, level):
global level_depth, x
level_depth = max(level_depth, level)
if node.left != -1:
in_order(tree[node.left_node],level+1)
level_min[level] = min(level_min[level], x)
level_max[level] - max(level_min[level],x)
x+=1
if node.right_node != -1:
in_order(tree[node.right_node], level+1)
n = int(input())
tree={}
level_min = [n]
level_max = [0]
level_min=[n]
level_max = [0]
root = -1
level_max = [0]
root =-1
x= 1
level_depth = 1
for i in range(1, n+1):
tree[i] = Node(i,-1,-1)
level_min.append(n)
level_max.append(0)
for _ in range(n):
number, left_node, right_node = map(int, input().split())
tree[number].left_node = left_node
tree[number].right_node = right_node
if left_node != -1:
tree[left_node].parent = number
if right_node != -1:
tree[right_node].parent = number
for i in range(1, n+1):
if tree[i].parent == -1:
root =i
in_order(tree[root], 1)
result_level = 1
result_width = level_max[1] - level_min[1]+1
for i in range(2, level_dept +1):
width = level_max[i] - level_min[i] +1
if result_width < width:
result_level = i
result_width = width
print(result_level, result_width)
n
'알고리즘' 카테고리의 다른 글
| 백준 1927번 최소힙 파이썬 (0) | 2020.10.12 |
|---|---|
| max heap 구현 파이썬 (0) | 2020.10.12 |
| 백준 1991 트리 순회 파이썬 (0) | 2020.10.07 |
| 코딜리티 3: TapeEquilibrium (0) | 2020.10.06 |
| 백준 1744번 수묶기 파이썬 (0) | 2020.10.05 |
