반응형
** 힙 구현**
- 일반적으로 힙 구현시 배열 자료구조를 활용한다.
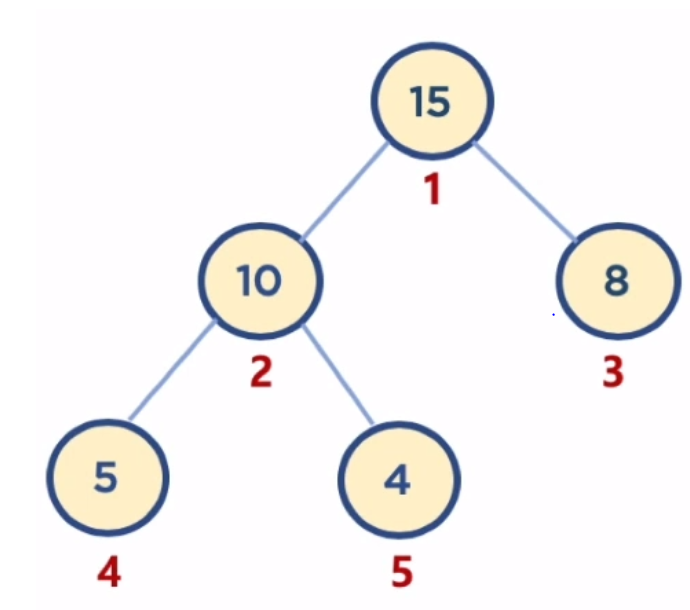
- 배열은 인덱스가 0번부터 시작하지만, 힙 구현의 편의를 위해 root 노드 인덱스 번호를 1로 지정하면, 구현이 좀더 수월하다.
- 부모 노드 인덱스 번호 = 자식 노드 인덱스 번호 //2
- 왼쪽자식 노드 인덱스 번호 = 부모노드 인덱스 번호 *2
- 오른쪽 자식 노드 인덱스 번호 = 부모노드 인덱스 번호 * 2+ 1
heap = Heap(15)
heap.insert(10)
heap.insert(8)
heap.insert(5)
heap.insert(4)
heap.insert(20)
heap.heap_array
heap.pop() # 20
# [None, 20, 10, 15, 5, 4, 8]class Heap:
def __init__(self, data):
self.heap_array = list()
self.heap_array.append(None)
self.heap_array.append(data)
def move_up(self, inserted_idx):
if inserted_idx<=1:
return False
parent_idx = inserted_idx //2
if self.heap_array[inserted_idx]> self.heap_array[parent_idx]:
return True
else:
return False
def insert(self, data):
if len(self.heap_array) ==0:
self.heap_array.append(None)
self.heap_array.append(data)
return True
self.heap_array.append(data)
inserted_idx = len(self.heap_array)-1
while self.move_up(inserted_idx): # 부모노드와의 비교
parent_idx = inserted_idx//2
self.heap_array[inserted_idx] , self.heap_array[parent_idx]=self.heap_array[parent_idx],self.heap_array[inserted_idx]
inserted_idx=parent_idx
return True
def move_down(self, popped_idx):
left_child_popped_idx = popped_idx*2
right_child_popped_idx = popped_idx*2+1
# case 1: 왼쪽 자식 노드도 없을때
if left_child_popped_idx >=len(self.heap_array):
return False
# case 2: 오른쪽 자식 노드만 없을때
elif right_child_popped_idx >=len(self.heap_array):
if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
return True
else:
return False
# case 3: 왼쪽, 오르쪽 자식 모두 있을때
else:
# 왼쪽이 더 큰경우
if self.heap_array[left_child_popped_idx]> self.heap_array[right_child_popped_idx]:
if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
return True
else:
return False
else:
# 오른쪽이 더 큰 경우
if self.heap_array[popped_idx] < self.heap_array[right_child_popped_idx]:
return True
else:
return False
def pop(self):
# 원리: 맥스힙의 pop 은 root 를 삭제하는 것이다.
# 구현 원리는 맨 최상단 root 를 tail 위치의 노드를 복사해 넣고, 마지막 노드를 삭제한 후, 정렬을 해주면 된다.
if len(self.heap_array)<=1: # pop 할것이 없는 루트 노드
return None
returned_data = self.heap_array[1]
self.heap_array[1] =self.heap_array[-1]
del self.heap_array[-1]
popped_idx =1
while self.move_down( popped_idx):
left_child_popped_idx = popped_idx*2
right_child_popped_idx = popped_idx*2+1
# case 1: 왼쪽 자식 노드도 없을때
if left_child_popped_idx >=len(self.heap_array):
pass # 신경 안쓰면 됨
# case 2: 오른쪽 자식 노드만 없을때
elif right_child_popped_idx >=len(self.heap_array):
if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
self.heap_array[popped_idx],self.heap_array[left_child_popped_idx]=self.heap_array[left_child_popped_idx],self.heap_array[popped_idx]
popped_idx=left_child_popped_idx
# case 3: 왼쪽, 오르쪽 자식 모두 있을때
else:
# 왼쪽이 더 큰경우
if self.heap_array[left_child_popped_idx]> self.heap_array[right_child_popped_idx]:
if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
self.heap_array[popped_idx],self.heap_array[left_child_popped_idx]=self.heap_array[left_child_popped_idx],self.heap_array[popped_idx]
popped_idx=left_child_popped_idx
else:
# 오른쪽이 더 큰 경우
if self.heap_array[popped_idx] < self.heap_array[right_child_popped_idx]:
self.heap_array[popped_idx],self.heap_array[right_child_popped_idx]=self.heap_array[right_child_popped_idx],self.heap_array[popped_idx]
popped_idx=right_child_popped_idx
return returned_data
힙(Heap) 시간복잡도
- depth (트리의 높이) 를 h 라고 표기한다면
- n 개의 노드를 가지는 heap 에 데이터 삽입 또는 삭제시, 최악의 경우 root 노드에서 leaf 노드까지 비교해야하므로 h = log2n 에 가까우니까 시간복잡도는 O(logn)
- 참고: 빅오표기법에서 logn 에서의 log 의 밑은 10이 아니라 2
- 한번 실행시마다 50 % 의 실행할 수도 있는 명령을 제거한다는 의미. 즉, 50 % 의 실행시간을 단축시킬수 있는 것을 의미함.
반응형
'알고리즘' 카테고리의 다른 글
| 백준 1715번 카드 정렬하기 (0) | 2020.10.12 |
|---|---|
| 백준 1927번 최소힙 파이썬 (0) | 2020.10.12 |
| 백준 트리의 높이와 너비 2250번 파이썬 (0) | 2020.10.07 |
| 백준 1991 트리 순회 파이썬 (0) | 2020.10.07 |
| 코딜리티 3: TapeEquilibrium (0) | 2020.10.06 |
